Na podstawie łamigłówki:
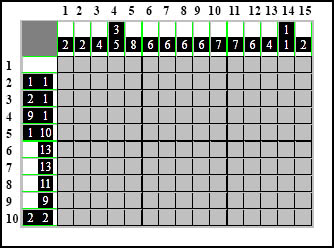
którą można także znaleźć tutaj:
Napiszę mały kurs rozwiązywania obrazków logicznych poprzez rozwiązanie jej krok po kroku.
Na obrazku wyżej zaznaczyłem wiersze - po lewej stronie od 1 do 10 oraz kolumny - na górze od 1 do 15.
Zaczynamy.
Zwykle zaczyna się rozwiązywać obrazek logiczny od miejsca, w którym jest najwięcej zajętych pól przez jak najmniejszą liczbę elementów.
Czyli interesują nas przede wszystkim największe liczby w wierszach i kolumnach łamigłówki.
Na naszym przykładzie jest kilka wierszy z dużymi liczbami i całkiem sporo kolumn.
Np.: w czwartym wierszu od góry mamy cyfry 9 i 1. To już wystarcza, żeby odgadnąć pewne kratki. Odnajdziemy je - ja to nazywam "Metodą Zazębienia" (MZ).
Polega ona na tym, że najpierw odliczamy na diagramie sekwencję cyfr od jednej strony, a potem od drugiej.
Tak więc, jeśli w czwartym wierszu pierwszą cyfrą jest 9 to oznacza to, że najbliżej lewej strony w tym wierszu będzie znajdował się element składający się z dziewięciu kratek, a za nim element jednokratkowy.
Najpierw zakładamy, że oba elementy stoją maksymalnie ściśnięte po jednej ze stron - my zaczniemy od lewej strony. Zaznaczamy najpierw dziewiątkę
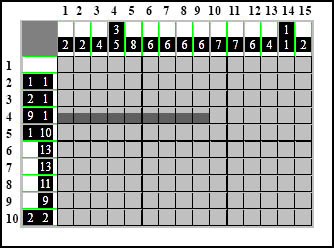
następnie przynajmniej jedna kratka odstępu, żeby elementy się nie zlały ze sobą i kolejny element jednokratkowy
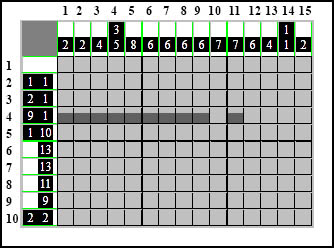
Teraz to samo tylko z drugiej strony - zakładamy, że oba elementy leżą maksymalnie ściśnięte po prawej stronie.
Zaczynamy od jedynki bo ona od prawej jest pierwsza a za nią jest dziewiątka czyli:
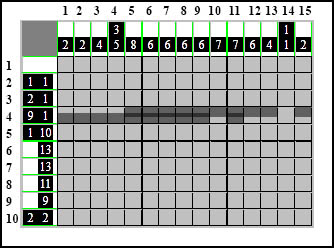
Oznaczę elementy cyframi dla lepszej orientacji:
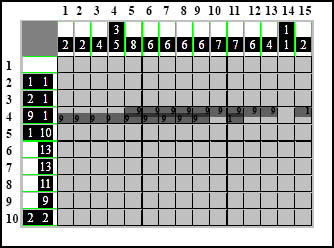
Metoda polega na oznaczeniu kratek, wynikających z zazębiających się tych samych elementów.
Na naszym diagramie widać wyraźnie, że jedynie element 9-kratkowy ustawiony maksymalnie od lewej i prawej strony zazębia się w pewnym miejscu diagramu:
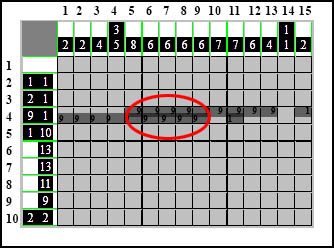
Element 1-kratkowy natomiast nie zazębia się. Raz jest w jednym miejscu, przy drugim założeniu w innym.
Zaznaczamy kratki tylko te, których jesteśmy pewni a pewność tą daje nam w przykładzie element 9-kratkowy, który niezależnie od tego gdzie ustawimy w wierszu, na pewno zasłoni sobą pewne - ściśle określone kratki - tego obrazka. Zasłoni ich oczywiście dziewięć - bo taką ma wielkość, ale pięć kratek zasłoni na pewno w ściśle określonym miejscu. To jest pewne więc zaznaczamy je:
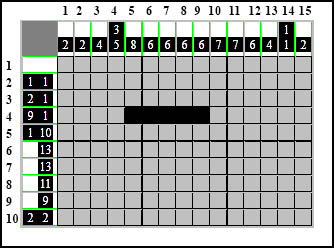
Przechodzimy do następnego - piątego wiersza, gdzie również znajdujemy wielkie cyfry (w stosunku do wielkości wiersza/kolumny w którym się znajdują).
I znowu Metodą Zazębiania (MZ) próbujemy odnaleźć kratki, których będziemy pewni.
Najpierw jedna strona - tym razem pierwszy jest element 1-kratkowy a za nim 10-kratkowy:
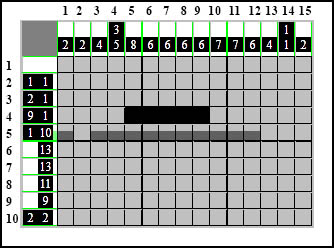
Następnie kolejna strona:
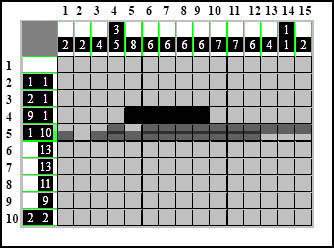
I ponownie widzimy, że zazębia się tylko jeden z elementów:
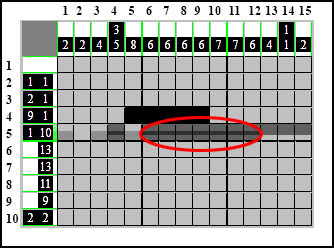
Zaznaczamy to miejsce:
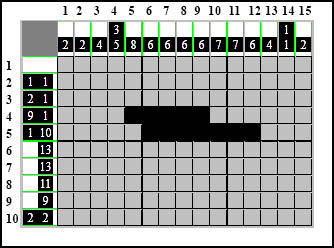
Podobnie czynimy z wierszami 6,7,8 i 9:
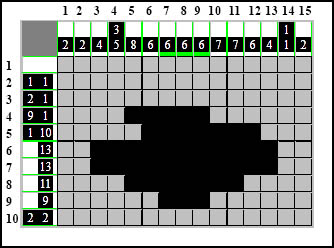
A teraz spróbujmy wykorzystać Metodę Zazębiania (MZ) w ostatnim - dziesiątym wierszu. Najpierw zaznaczamy elementy ściśnięte z jednej strony:
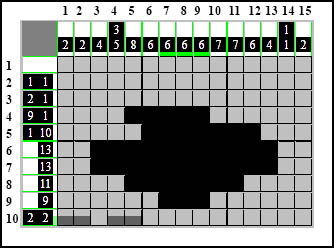
Następnie z drugiej:
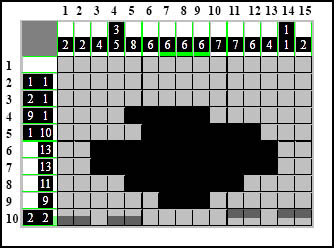
Jak widać żaden z elementów nie zazębia się i nie można niczego zaznaczyć. Metoda Zazębiania najczęściej przydaje się kiedy elementy są większej wielkości.
Spójrzmy jeszcze na wiersz pierwszy łamigłówki. Nie zawiera on żadnych cyfr. Oznacza to, że nie ma w nim żadnych elementów i możemy oznaczyć go kolorem tła - lub inaczej kolorem ukrytym, ponieważ jest to kolor, którego w łamigłówce nie opisują żadne cyfry. Dzięki temu pozostałych kolorów trzeba się domyślić, wydedukować.
Oznaczamy więc nasz wiersz pierwszy kolorem tła, który w przypadku tego obrazka logicznego jest biały:
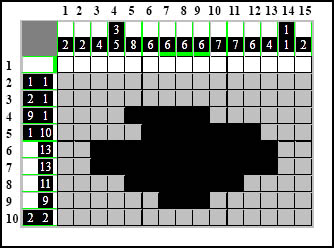
Spójrzmy teraz na kolumny 7,8 i 9. Zawierają one po jednym elemencie 6-kratkowym każda. Przez nasze rysowanie w wierszach, zamalowaliśmy i kolumny. Jeśli uważnie policzymy, to w kolumnach 7, 8 i 9 jest dokładnie tyle kratek ile powinno być i nie można już niczego więcej domalować. Oznacza to tyle, że pozostałe puste kratki w tych kolumnach muszą należeć do tła - więc zamalowujemy je na biało:
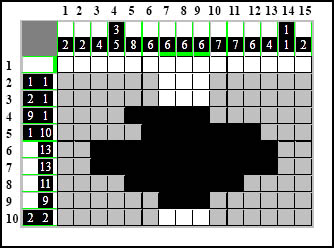
Tak działa "Metoda Zazębiania". Przejdźmy do kolejnej, którą nazwiemy "Uzupełnij Przy Brzegach" (UPB).
- Jeśli zdobyliśmy jakieś kratki na tyle blisko brzegu diagramu, aby "zahaczył" je najbliższy tego brzegu element, to kratki te na pewno należą do tego elementu i ponadto można je przedłużyć o długość tego elementu.
Jak to wygląda w praktyce...
Przyjrzyjmy się naszemu diagramowi w kolumnie Piątej.
W wyniku rysowania w wierszach, zdobyliśmy także czarne kratki i w kolumnie piątej. Dokładnie jest ich dwie grupy. Pierwsza grupa składa się z jednej kratki a druga z trzech.
Ponieważ w tej kolumnie jest tylko jeden element, to już wiemy, że i grup powinno być nie dwie a jedna więc śmiało połączyć można wszystkie kratki razem.
Ale można też zrobić znacznie więcej i do tego celu użyjemy metody "Uzupełnij Przy Brzegach" (UPB).
Te wspomniane grupy kratek w kolumnie piątej znalazły się tak blisko brzegu diagramu, że na pewno "zahaczy je" sobą element (a jest w tej kolumnie tylko jeden element 8-kratkowy) przy założeniu (co bardzo istotne), że zacznie się on jak najbliżej brzegu diagramu - czyli w naszym przypadku od pozycji drugiej, ponieważ pierwsze pole w tej kolumnie jest już białe.
Zaczynamy liczyć. Mamy dwa pola puste, następnie jedno czarne. Ich suma to trzy pola a nasz element składa się z ośmiu. Oznacza to, że pierwsza grupa kratek składająca się z jednej kratki należy do elementu 8-kratkowego i można ją przedłużyć o kolejne kratki.
liczymy więc dalej:
Kolejne puste pole - zamalowujemy:
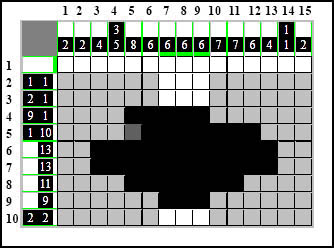
- nasza suma to już cztery, brakuje jeszcze kolejne cztery. I wchodzimy w następną grupę kratek co oznacza zgodnie z zasadą, że i ona należy do najbliższego elementu, ponieważ "zahaczył" ją sobą, więc doliczamy ją co daje w sumie wynik siedem. My natomiast wiemy, że najbliższy element składa się z ośmiu kratek, więc i tak jeszcze brakuje jednej. Również zgodnie z zasadą, możemy przedłużyć te kratki o brakującą ostatnią kratkę:
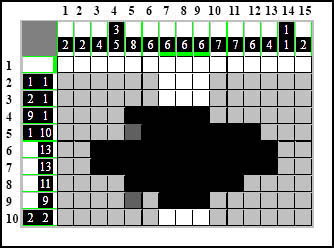
Teraz wszystko się zgadza i możemy zatwierdzić nasz ruch:
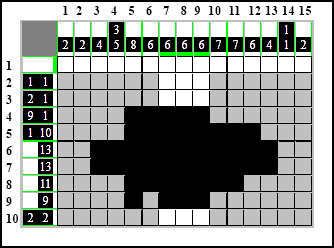
Tą samą metodę użyjemy w tej samej kolumnie piątej, lecz z drugiej strony:
Liczymy: jedno puste pole, potem grupa sześciu kratek, którą zahacza element - razem siedem kratek. Brakuje jeszcze jednej i doliczamy ją:
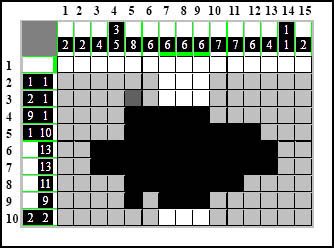
wszystko się zgadza więc zatwierdzamy:
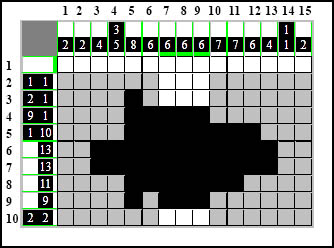
Tej samej metody użyjemy również w wierszu dziewiątym, gdzie mamy jeden element 9-kratkowy a na diagramie powstały dwie grupy.
Po przeliczeniu okazuje się, że obie grupy "zahacza" ten element i można je połączyć:
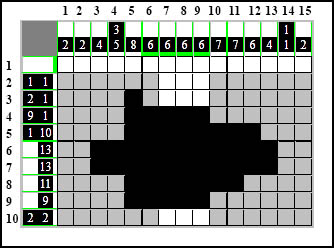
Ponadto wiemy, że teraz grupa 5-kratkowa, jaka powstała w wyniku połączenia należy właśnie do elementu 9-kratkowego, co będzie stanowiło wyjście do kolejnej metody, którą nazwiemy "Uzupełnij Luki Pomiędzy Elementami" (ULPE).
Luki można uzupełnić pomiędzy dwoma elementami lub pomiędzy jednym elementem a brzegiem diagramu. Żeby to zrobić, musimy wiedzieć dokładnie o jakie elementy chodzi.
Z ostatnich naszych poczynań stwierdziliśmy, że w dziewiątym wierszu grupa pięciu kratek na naszym obrazku logicznym należy do elementu 9-kratkowego.
Oznacza to, że brakujące cztery kratki możemy domalować z lewej, z prawej lub z obydwu jej stron. Jednak my skupimy się jak zwykle na założeniach...
Mało da nam pożytku założenie, że domalowujemy kratki z obu stron grupy. Załóżmy lepiej, że koniec 9-kratkowego elementu znajduje się na ostatniej - w tym wierszu to będzie na dziewiątej kratce. Wszystkie brakujące będziemy musieli wtedy domalować po lewej stronie grupy. Potrzeba nam jeszcze cztery kratki i jeśli dodamy je do grupy to okaże się, że skończyliśmy dokładnie na samym początku diagramu. Niewiele to nam daje... Jednak teraz załóżmy odwrotnie. To znaczy, że koniec naszego elementu teraz znajduje się na pierwszej kratce należącej do grupy pięciu kratek. Doliczmy pozostałe cztery kratki po drugiej stronie grupy...
Widać wyraźnie, że jest tam jeszcze jakiś odstęp - dokładnie brakuje jeszcze dwóch kratek do brzegu diagramu.
Dla nas wynika z tego ważna informacja.
- Te dwie kratki to "pewniak". Nigdy nie będą one w innym kolorze niż biały, ponieważ nasz element 9-kratkowy jest po prostu za krótki i nie dosięgnie ich nawet jeśli będzie zaczynał się z miejsca najbardziej wysuniętego na prawo w tym wierszu - nic to mu nie da. Możemy więc zamalować te kratki na biało:
Białe kratki też mają ogromne znaczenie i nie należy ich lekceważyć. Czasami postawienie jednej białej kratki pozwala przełamać impas a nierzadko determinuje rozwiązanie.
Idźmy więc dalej śladem białych kratek, bo one prowadzą nas do kolejnej metody: "Uzupełnij Najmniejsze Luki" (UNL). Taki tytuł jej nadamy, choć w rzeczywistości rozwiązując obrazki logiczne nigdy nie myśli się nad tym jakiej metody się używa;] Po prostu myślimy "automatycznie", podświadomie wybierając odpowiednie mechanizmy. Kierując się logiką w działaniu. Jednak teraz staram się wytłumaczyć mechanizmy myśleniowe, dać wskazówki i podpowiedzi. Zakładam, że potem każdy sam zmodyfikuje je dla swoich potrzeb i zaczniecie używać "w biegu" - bez zbędnego myślenia o nich samych.
Metoda, którą teraz przedstawiam - "Uzupełnij Najmniejsze Luki"(UNL) polega na zamalowywaniu małych grup pustych kratek w łamigłówce kolorem tła - u nas białym. Te małe luki pustych kratek (czyli ani czarnych, ani białych w naszym przypadku) muszą być małe w pewnym znaczeniu. Dokładnie - muszą być mniejsze od najmniejszego elementu w linii, którą sprawdzamy.
A teraz praktyka.
Przyjrzyjmy się kolumnie piętnastej. Znajduje się w niej tylko jeden element 2-kratkowy. Natomiast przez domalowanie białych okienek w dziewiątym wierszu spowodowaliśmy, że w kolumnie 15 powstała mała grupa pustych kratek. Dokładnie grupa 1-kratkowa na samym końcu tej kolumny. Ta grupa jest mniejsza od najmniejszego elementu w kolumnie piętnastej, który ma wielkość dwóch kratek. One się tam po prostu już nie zmieszczą! Możemy więc to miejsce zamalować na biało, ponieważ jest to pewne.
I to cała filozofia metody UNL.
Natomiast w kolumnie obok - w czternastej - nie możemy już tego zrobić, ponieważ tam najmniejszym elementem jest element 1-kratkowy i może on śmiało zmieścić się w pustym miejscu, które powstało na końcu tej pionowej linii. My zaznaczamy tylko rzeczy, których jesteśmy pewni na 100%.
Przejdźmy jednak do kolumny jeszcze wcześniejszej - do trzynastej i tam użyjmy metody "Uzupełnij Luki Pomiędzy Elementami"
Jak już zaznaczyłem, żeby skorzystać z tej metody potrzebna nam jest wiedza do jakiego elementu należy grupa kratek lub do jakich elementów - jeśli mamy zamiar zamalowywać puste miejsca pomiędzy elementami - czego w tym obrazku logicznym nie zrobimy, bo jest zbyt mało skomplikowany. Jednak zasada jest ta sama - zamalowujemy kratki poza zasięgiem elementów.
W kolumnie trzynastej możemy na dwa sposoby przekonać się, że grupa dwóch kratek należy do elementu 4-kratkowego.
Po pierwsze jest to jedyny element w tej kolumnie więc i grupa musi należeć do niego
Po drugie, jeśli skorzystamy z metody UPB (Uzupełnij Przy Przegach) i policzymy element maksymalnie od dołu w 13 wierszu, to "zahaczy" on sobą grupę dwóch kratek co oznacza, że ona po prostu do niego należy.
Skoro już wiemy z jakim elementem mamy do czynienia, użyjmy metody ULPE (Uzupełnij Luki Pomiędzy Elementami) w wariancie, że będziemy uzupełniać te luki pomiędzy jednym elementem a brzegiem diagramu.
Czyli najpierw załóżmy, że element zaczyna się od dolnego miejsca, w którym zaczyna się grupa dwóch kratek - to jest od kratki czwartej licząc od dołu. Dodajemy brakujące dwie kratki i okazuje się, że elementowi zabraknie jeszcze dwóch kratek do krawędzi:
Teraz to samo tylko z przeciwnej strony: Zakładamy, że element zaczyna się od górnego miejsca grupy - to jest od szóstej kratki licząc od góry. Jak widać do końca braknie mu jeszcze jedna kratka, którą oczywiście zamalowujemy.
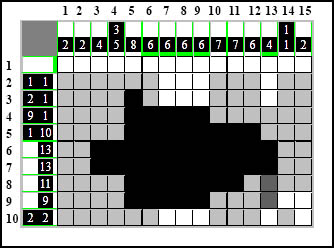
I znowu metoda UNL w wierszu dziesiątym.
Przez dodanie białej kratki w kolumnie trzynastej stworzyliśmy pustą lukę jednokratkową w wierszu dziasiątym, podczas gdy w tym wierszu najmniejszy element ma wartość 2 i nie zmieści się w luce. Zamalowujemy więc i to miejsce:
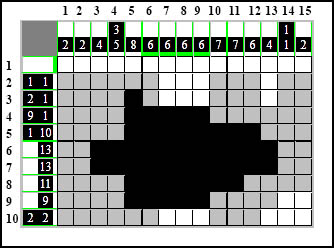
Powróćmy teraz na sam początek - do pierwszej metody "zazębiania" (MZ) i spróbujmy ją wykorzystać do oznaczenia elementów w dziesiątym wierszu, ponieważ przez to nasze domalowywanie, miejsca się w nim robi coraz mniej.
Najpierw jeden skraj - zaznaczamy dwa elementy każdy po dwie kratki:
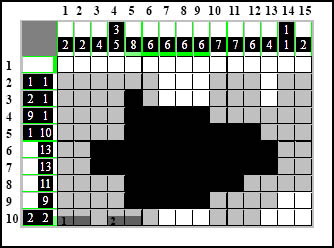
Następnie druga strona, jak widać miejsca już nie starcza, aby ustawić dwa elementy obok siebie, jeden z nich trzeba przenieść dalej aby oba mogły się zmieścić.
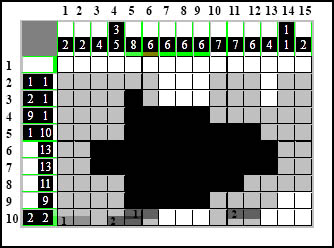
Teraz sprawdzamy czy coś się zazębiło.
Zazębiło się, ale niestety nie to co chcieliśmy, ponieważ jak wiemy muszą się zazębiać te same elementy a nie różne.
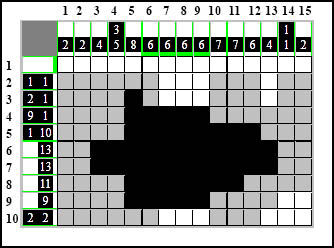
Ponownie nic w tym wierszu teraz nie zaznaczymy. Musimy zaczekać jeszcze trochę.
Do tej pory poznaliśmy cztery podstawowe metody, które dodatkowo można rozbudowywać i modyfikować co spowoduje, że będziemy w stanie korzystając z nich rozwiązać znakomitą większość obrazków logicznych.
Metody te to:
1) Metoda Zazębiania (MZ).
2) Uzupełnij Przy Brzegach (UPB).
3) Uzupełnij Najmniejsze Luki (UNL).
4) Uzupełnij Luki Pomiędzy Elementami (ULPE).
Wracamy do malowania liczbami.
Ostatnio próbowaliśmy zdobyć jakieś kratki w ostatnim - 10 wierszu, lecz było na to jeszcze za wcześnie.
Przyjrzyjmy się jednak kolumnie czwartej z dwoma elementami - 3-kratkowym oraz 5-kratkowym.
Wykorzystajmy MZ ponownie. Licząc od skrajnej góry. Najpierw 3-kratkowy element:
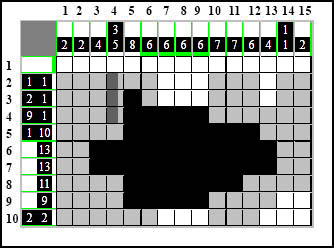
Potem kratka odstępu i kolejny - drugi element 5-kratkowy - oba ściśnięte maksymalnie na górze:
Oznaczę cyframi dodatkowo dla lepszej widoczności:
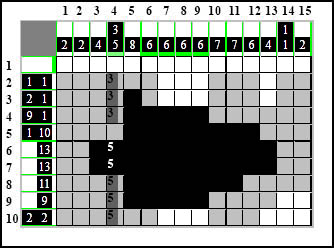
Widać wyraźnie, że nawet maksymalnie ściśnięte zajmują sobą calutką linię co do jednej kratki. Właściwie nie trzeba już wcale liczyć od drugiej strony - po prostu nie ma innej możliwości ale oznaczmy to dla formalności. Czyli najpierw piątka od dołu a za nią trójka.
Oba zazębiają się w całości, nie pozostaje nic innego jak zaznaczyć to:
W drugim wierszu mamy same elementy o wielkości jednej kratki. Możemy więc w tym wierszu kratkę czarną - jaką przed chwilą zamalowaliśmy - dodatkowo obłożyć kratkami białymi z obu stron. Natomiast w wierszu trzecim widać, że powstał element 2-kratkowy, który z kolei jest pierwszy od lewej. Oznacza to, że mało tego iż możemy obwarować go białymi kratkami z obu stron (ponieważ wiemy, że to na pewno o niego chodzi) to jeszcze możemy uzupełnić białe kratki aż do samej lewej krawędzi diagramu - po prostu przed nim nie ma już nic innego:
Nie możemy namalować białych kratek z drugiej strony, ponieważ za elementem 2-kratkowym znajduje się 1-kratkowy i nie mamy pojęcia jeszcze gdzie on może być.
Dokładnie to samo dotyczy wiersza drugiego, gdzie powstało jedno puste pole, w które jednak zmieści się kolejny element 1-kratkowy w tym wierszu jednak...
Kiedy przyjrzymy się temu pustemu polu lecz z perspektywy szóstej kolumny, gdzie jest tylko jeden element 6-kratkowy, z łatwością wydedukujemy, że nie zmieści się tam szóstka i śmiało możemy zamalować puste miejsce (metoda uzupełnij najmniejsze luki).
Dodatkowo możemy uzupełnić tą kolumnę, ponieważ malując w wierszach uzupełniliśmy ją w całości do sześciu kratek.
Natomiast kiedy obwarowaliśmy element 1-kratkowy białymi kratkami z obu jego stron w wierszu drugim, jednocześnie postawiliśmy białą kratkę w kolumnie trzeciej i piątej. Ruchem tym sprawiliśmy, że teraz jedyne miejsce jakie zostało w piątej kolumnie zajmie do końca element 8-kratkowy.
Uzupełnienie nim linii do końca spowodowało, że w ostatnim - dziesiątym wierszu pojawił się w pełni wykształtowany;] element 2-kratkowy. Ponieważ tam są same elementy 2 -kratkowe, śmiało i jego możemy obwarować białymi polami po obu stronach.
Czyli podsumowując uzupełniamy do końca kolumny 5 i 6 oraz obwarowujemy element 2-kratkowy w 10 wierszu:
Przechodzimy do wiersza piątego, gdzie postawiliśmy białą kratkę odstępu. Ruchem tym spowodowaliśmy, że czarny element 10-kratkowy teraz zaczyna się dokładnie od białego pola i nie pozostaje nic innego jak po prostu przedłużenie go do samego końca - czyli do pełnych dziesięciu kratek. (jest to rozwinięcie metody "uzupełnij przy brzegach" - w tym przypadku brzeg stanowi ta biała kratka, o której wiemy, że na pewno stoi od lewej strony elementu 10-kratkowego, może zatem stanowić jego brzeg).
Przedłużamy więc:
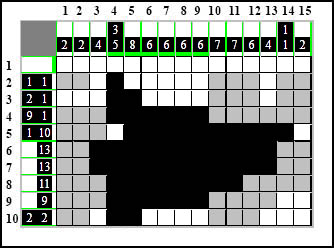
Jedynkę po lewej stronie dziesiątki w tym wierszu natomiast nie wiemy jeszcze gdzie postawić, zostawiamy ją w spokoju.
Uzupełnienie elementu 10-kratkowego w wierszu piątym spowodowało pojawienie się jednej czarnej kratki w kolumnie czternastej, a ponieważ tam są same elementy 1-kratkowe, podobnie jak już to robiliśmy wcześniej, obwarowujemy czarne pole białymi po obu stronach.
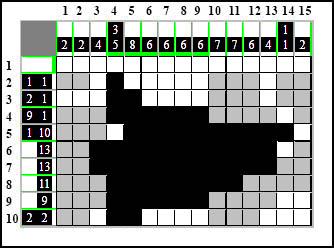
Białe pola jak już wcześniej wspomniałem są tak samo ważne jak i czarne. W naszym przypadku postawienie białego pola w kolumnie czternastej spowodowało zablokowanie elementu 13-kratkowego w wierszu szóstym. Od tej pory nie ma on innej możliwości jak "iść" jedynie w lewą stronę. I tak go właśnie przedłużamy w lewo aż do samej jego długości, ponieważ dotyka go już brzeg z prawej strony.
Natomiast korzystając z metody ULPE w kolumnie pierwszej możemy oznaczyć białe kratki z jednej i drugiej strony grupy 1-kratkowej która się tu pojawiła:
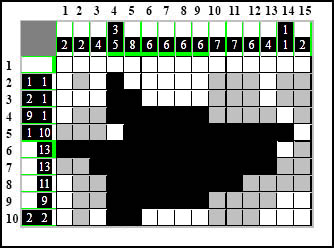
Teraz już wiemy, że w dziesiątym wierszu na początku nie ma już miejsca na element 2-kratkowy i puste pole zamalowujemy na biało, natomiast korzystając z MZ oznaczamy część drugiego elementu 2-kratkowego w tym wierszu:
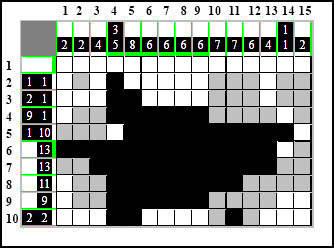
Metoda UPB i mamy calutką kolumnę jedenastą:
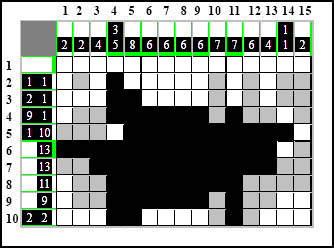
Skorzystajmy z tej samej metody w wierszu czwartym i policzmy od lewej element 9-kratkowy.
Najpierw dwa pola puste, potem sześć czarnych - razem osiem kratek. Brakuje jeszcze jednej. Ostatnia kratka wypada dokładnie pomiędzy grupą sześciu kratek i grupą jednokratkową. I nie ma innej możliwości na dodatek. Nie można już bardziej przesunąć w lewą stronę liczenia tak, żeby grupy pozostały osobno. Trzeba je po prostu połączyć ze sobą bo muszą należeć do elementu 9-kratkowego. W ten sposób, kiedy połączymy te grupy i korzystając z metody Uzupełnij Luki Pomiędzy Elementami" (w wariancie pomiędzy elementem i brzegiem), możemy domalować białe pole na początku tego wiersza:
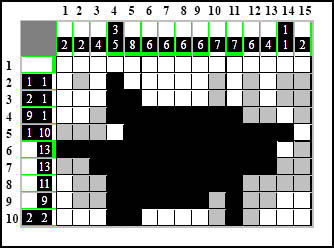
Korzystając z tej samej metody uzupełniamy pola przy brzegach w kolumnie drugiej:
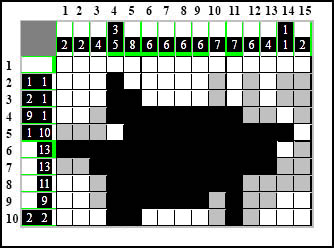
A potem metodą UPB uzupełniamy kratki w wierszach 8 i 9:
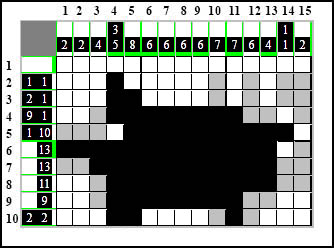
Teraz kolumna trzynasta... widzimy, że manewrami w wierszach doprowadziliśmy ją do końca - pojawił się w pełni wykształtowany;] element 4-kratkowy więc uzupełniamy resztę białymi polami:
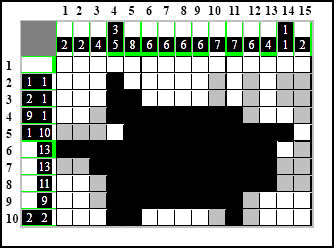
Domalowanie przed chwilą białego pola w wierszu czwartym spowodowało, że pozostało już tylko jedno miejsce dla elementu 1-kratkowego więc go tam oznaczamy:
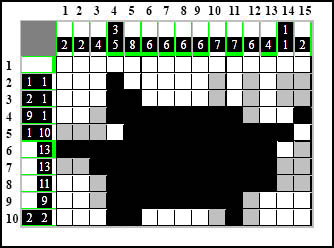
Ta kratka to zalążek elementu 2-kratkowego, na dodatek jedynego w kolumnie piętnastej, i na dodatek kratka ta zaczyna się od białego pola - a więc nie ma innej możliwości jak oznaczenie tego elementu w pełni oraz uzupełnienie kolumny białymi polami do końca:
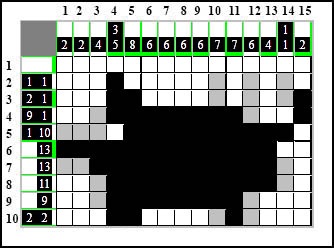
Uzupełnienie piętnastej kolumny spowodowało pojawienie się czarnej kratki w wierszu trzecim a to oznacza, że pojawił się ostatni element w tym wierszu i resztę można zamalować na biało:
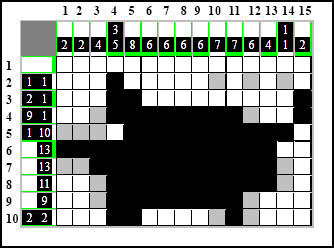
Kolumna dziesiąta - zamalowujemy puste pole bo nie zmieści się tam 7-kratkowy element.
W kolumnie dwunastej robimy to samo. Dzięki temu w wierszu drugim pozostało ostatnie pole na ostatni element 1-kratkowy. Oznaczamy to wszystko:
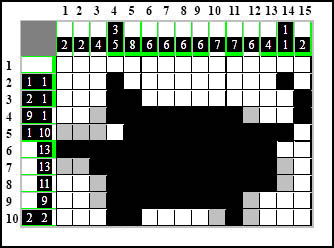
Pojawia się ostatni element w kolumnie czternastej - uzupełniamy resztę białymi polami.
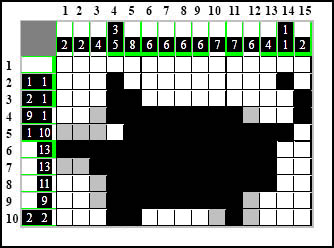
Wszystko teraz pędzi z dużą prędkością i widać już metę...
Domalowane przed chwilą białe kratki blokują elementy w siódmym i ósmym wierszu, przez co możemy je przedłużyć do samego ich końca:
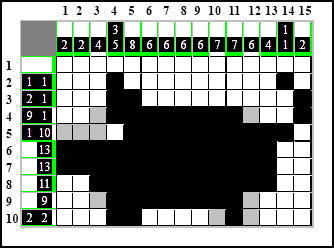
Pojawiają się końcowe elementy w pierwszej i drugiej kolumnie, uzupełniamy je:
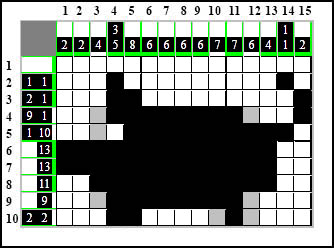
Korzystamy z metody ULPE w kolumnie trzeciej licząc od dołu element 4-kratkowy i wyciskamy tym sposobem białą kratkę na górze tej kolumny:
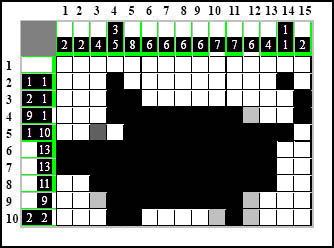
Dzięki tej białej kratce uzupełniamy do końca wiersz czwarty:
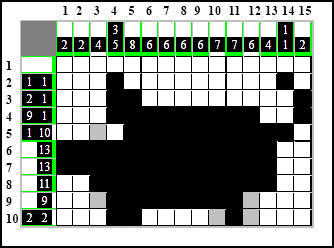
A potem kolumnę dwunastą:
To pozwala nam uzupełnić do końca wiersze dziewiąty oraz dziesiąty:
Pozostaje ostatnie jedno puste pole, na ostatni element 1-kratkowy w wierszu piątym lub na dokończenie elementu 4-kratkowego w kolumnie trzeciej. Wszystko się zgadza!
No i nasza łamigłówka okazała się... ŚWINIĄ!;]
Kurs starałem się pisać przystępnie, krok po kroku.
Poznaliśmy w nim kilka ciekawych metod/sposobów myślenia/dedukcji - jak kto woli.
Teraz wystarczy zmodyfikować je nieco, ulepszyć, rozwinąć... no i bawić się rozwiązując kolejne obrazki logiczne!
I tego życzę wszystkim serdecznie na koniec.
Marcin Rejment
którą można także znaleźć tutaj:
Napiszę mały kurs rozwiązywania obrazków logicznych poprzez rozwiązanie jej krok po kroku.
Na obrazku wyżej zaznaczyłem wiersze - po lewej stronie od 1 do 10 oraz kolumny - na górze od 1 do 15.
Zaczynamy.
Zwykle zaczyna się rozwiązywać obrazek logiczny od miejsca, w którym jest najwięcej zajętych pól przez jak najmniejszą liczbę elementów.
Czyli interesują nas przede wszystkim największe liczby w wierszach i kolumnach łamigłówki.
Na naszym przykładzie jest kilka wierszy z dużymi liczbami i całkiem sporo kolumn.
Np.: w czwartym wierszu od góry mamy cyfry 9 i 1. To już wystarcza, żeby odgadnąć pewne kratki. Odnajdziemy je - ja to nazywam "Metodą Zazębienia" (MZ).
Polega ona na tym, że najpierw odliczamy na diagramie sekwencję cyfr od jednej strony, a potem od drugiej.
Tak więc, jeśli w czwartym wierszu pierwszą cyfrą jest 9 to oznacza to, że najbliżej lewej strony w tym wierszu będzie znajdował się element składający się z dziewięciu kratek, a za nim element jednokratkowy.
Najpierw zakładamy, że oba elementy stoją maksymalnie ściśnięte po jednej ze stron - my zaczniemy od lewej strony. Zaznaczamy najpierw dziewiątkę
następnie przynajmniej jedna kratka odstępu, żeby elementy się nie zlały ze sobą i kolejny element jednokratkowy
Teraz to samo tylko z drugiej strony - zakładamy, że oba elementy leżą maksymalnie ściśnięte po prawej stronie.
Zaczynamy od jedynki bo ona od prawej jest pierwsza a za nią jest dziewiątka czyli:
Oznaczę elementy cyframi dla lepszej orientacji:
Metoda polega na oznaczeniu kratek, wynikających z zazębiających się tych samych elementów.
Na naszym diagramie widać wyraźnie, że jedynie element 9-kratkowy ustawiony maksymalnie od lewej i prawej strony zazębia się w pewnym miejscu diagramu:
Element 1-kratkowy natomiast nie zazębia się. Raz jest w jednym miejscu, przy drugim założeniu w innym.
Zaznaczamy kratki tylko te, których jesteśmy pewni a pewność tą daje nam w przykładzie element 9-kratkowy, który niezależnie od tego gdzie ustawimy w wierszu, na pewno zasłoni sobą pewne - ściśle określone kratki - tego obrazka. Zasłoni ich oczywiście dziewięć - bo taką ma wielkość, ale pięć kratek zasłoni na pewno w ściśle określonym miejscu. To jest pewne więc zaznaczamy je:
Przechodzimy do następnego - piątego wiersza, gdzie również znajdujemy wielkie cyfry (w stosunku do wielkości wiersza/kolumny w którym się znajdują).
I znowu Metodą Zazębiania (MZ) próbujemy odnaleźć kratki, których będziemy pewni.
Najpierw jedna strona - tym razem pierwszy jest element 1-kratkowy a za nim 10-kratkowy:
Następnie kolejna strona:
I ponownie widzimy, że zazębia się tylko jeden z elementów:
Zaznaczamy to miejsce:
Podobnie czynimy z wierszami 6,7,8 i 9:
A teraz spróbujmy wykorzystać Metodę Zazębiania (MZ) w ostatnim - dziesiątym wierszu. Najpierw zaznaczamy elementy ściśnięte z jednej strony:
Następnie z drugiej:
Jak widać żaden z elementów nie zazębia się i nie można niczego zaznaczyć. Metoda Zazębiania najczęściej przydaje się kiedy elementy są większej wielkości.
Spójrzmy jeszcze na wiersz pierwszy łamigłówki. Nie zawiera on żadnych cyfr. Oznacza to, że nie ma w nim żadnych elementów i możemy oznaczyć go kolorem tła - lub inaczej kolorem ukrytym, ponieważ jest to kolor, którego w łamigłówce nie opisują żadne cyfry. Dzięki temu pozostałych kolorów trzeba się domyślić, wydedukować.
Oznaczamy więc nasz wiersz pierwszy kolorem tła, który w przypadku tego obrazka logicznego jest biały:
Spójrzmy teraz na kolumny 7,8 i 9. Zawierają one po jednym elemencie 6-kratkowym każda. Przez nasze rysowanie w wierszach, zamalowaliśmy i kolumny. Jeśli uważnie policzymy, to w kolumnach 7, 8 i 9 jest dokładnie tyle kratek ile powinno być i nie można już niczego więcej domalować. Oznacza to tyle, że pozostałe puste kratki w tych kolumnach muszą należeć do tła - więc zamalowujemy je na biało:
Tak działa "Metoda Zazębiania". Przejdźmy do kolejnej, którą nazwiemy "Uzupełnij Przy Brzegach" (UPB).
- Jeśli zdobyliśmy jakieś kratki na tyle blisko brzegu diagramu, aby "zahaczył" je najbliższy tego brzegu element, to kratki te na pewno należą do tego elementu i ponadto można je przedłużyć o długość tego elementu.
Jak to wygląda w praktyce...
Przyjrzyjmy się naszemu diagramowi w kolumnie Piątej.
W wyniku rysowania w wierszach, zdobyliśmy także czarne kratki i w kolumnie piątej. Dokładnie jest ich dwie grupy. Pierwsza grupa składa się z jednej kratki a druga z trzech.
Ponieważ w tej kolumnie jest tylko jeden element, to już wiemy, że i grup powinno być nie dwie a jedna więc śmiało połączyć można wszystkie kratki razem.
Ale można też zrobić znacznie więcej i do tego celu użyjemy metody "Uzupełnij Przy Brzegach" (UPB).
Te wspomniane grupy kratek w kolumnie piątej znalazły się tak blisko brzegu diagramu, że na pewno "zahaczy je" sobą element (a jest w tej kolumnie tylko jeden element 8-kratkowy) przy założeniu (co bardzo istotne), że zacznie się on jak najbliżej brzegu diagramu - czyli w naszym przypadku od pozycji drugiej, ponieważ pierwsze pole w tej kolumnie jest już białe.
Zaczynamy liczyć. Mamy dwa pola puste, następnie jedno czarne. Ich suma to trzy pola a nasz element składa się z ośmiu. Oznacza to, że pierwsza grupa kratek składająca się z jednej kratki należy do elementu 8-kratkowego i można ją przedłużyć o kolejne kratki.
liczymy więc dalej:
Kolejne puste pole - zamalowujemy:
- nasza suma to już cztery, brakuje jeszcze kolejne cztery. I wchodzimy w następną grupę kratek co oznacza zgodnie z zasadą, że i ona należy do najbliższego elementu, ponieważ "zahaczył" ją sobą, więc doliczamy ją co daje w sumie wynik siedem. My natomiast wiemy, że najbliższy element składa się z ośmiu kratek, więc i tak jeszcze brakuje jednej. Również zgodnie z zasadą, możemy przedłużyć te kratki o brakującą ostatnią kratkę:
Teraz wszystko się zgadza i możemy zatwierdzić nasz ruch:
Tą samą metodę użyjemy w tej samej kolumnie piątej, lecz z drugiej strony:
Liczymy: jedno puste pole, potem grupa sześciu kratek, którą zahacza element - razem siedem kratek. Brakuje jeszcze jednej i doliczamy ją:
wszystko się zgadza więc zatwierdzamy:
Tej samej metody użyjemy również w wierszu dziewiątym, gdzie mamy jeden element 9-kratkowy a na diagramie powstały dwie grupy.
Po przeliczeniu okazuje się, że obie grupy "zahacza" ten element i można je połączyć:
Ponadto wiemy, że teraz grupa 5-kratkowa, jaka powstała w wyniku połączenia należy właśnie do elementu 9-kratkowego, co będzie stanowiło wyjście do kolejnej metody, którą nazwiemy "Uzupełnij Luki Pomiędzy Elementami" (ULPE).
Luki można uzupełnić pomiędzy dwoma elementami lub pomiędzy jednym elementem a brzegiem diagramu. Żeby to zrobić, musimy wiedzieć dokładnie o jakie elementy chodzi.
Z ostatnich naszych poczynań stwierdziliśmy, że w dziewiątym wierszu grupa pięciu kratek na naszym obrazku logicznym należy do elementu 9-kratkowego.
Oznacza to, że brakujące cztery kratki możemy domalować z lewej, z prawej lub z obydwu jej stron. Jednak my skupimy się jak zwykle na założeniach...
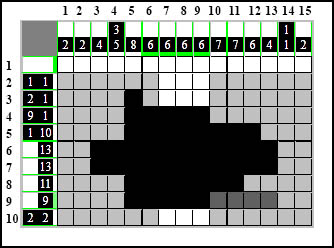
Mało da nam pożytku założenie, że domalowujemy kratki z obu stron grupy. Załóżmy lepiej, że koniec 9-kratkowego elementu znajduje się na ostatniej - w tym wierszu to będzie na dziewiątej kratce. Wszystkie brakujące będziemy musieli wtedy domalować po lewej stronie grupy. Potrzeba nam jeszcze cztery kratki i jeśli dodamy je do grupy to okaże się, że skończyliśmy dokładnie na samym początku diagramu. Niewiele to nam daje... Jednak teraz załóżmy odwrotnie. To znaczy, że koniec naszego elementu teraz znajduje się na pierwszej kratce należącej do grupy pięciu kratek. Doliczmy pozostałe cztery kratki po drugiej stronie grupy...
Widać wyraźnie, że jest tam jeszcze jakiś odstęp - dokładnie brakuje jeszcze dwóch kratek do brzegu diagramu.
Dla nas wynika z tego ważna informacja.
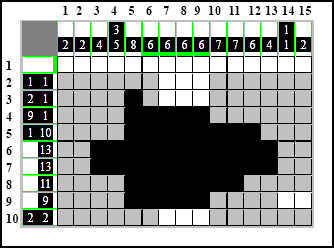
- Te dwie kratki to "pewniak". Nigdy nie będą one w innym kolorze niż biały, ponieważ nasz element 9-kratkowy jest po prostu za krótki i nie dosięgnie ich nawet jeśli będzie zaczynał się z miejsca najbardziej wysuniętego na prawo w tym wierszu - nic to mu nie da. Możemy więc zamalować te kratki na biało:
Białe kratki też mają ogromne znaczenie i nie należy ich lekceważyć. Czasami postawienie jednej białej kratki pozwala przełamać impas a nierzadko determinuje rozwiązanie.
Idźmy więc dalej śladem białych kratek, bo one prowadzą nas do kolejnej metody: "Uzupełnij Najmniejsze Luki" (UNL). Taki tytuł jej nadamy, choć w rzeczywistości rozwiązując obrazki logiczne nigdy nie myśli się nad tym jakiej metody się używa;] Po prostu myślimy "automatycznie", podświadomie wybierając odpowiednie mechanizmy. Kierując się logiką w działaniu. Jednak teraz staram się wytłumaczyć mechanizmy myśleniowe, dać wskazówki i podpowiedzi. Zakładam, że potem każdy sam zmodyfikuje je dla swoich potrzeb i zaczniecie używać "w biegu" - bez zbędnego myślenia o nich samych.
Metoda, którą teraz przedstawiam - "Uzupełnij Najmniejsze Luki"(UNL) polega na zamalowywaniu małych grup pustych kratek w łamigłówce kolorem tła - u nas białym. Te małe luki pustych kratek (czyli ani czarnych, ani białych w naszym przypadku) muszą być małe w pewnym znaczeniu. Dokładnie - muszą być mniejsze od najmniejszego elementu w linii, którą sprawdzamy.
A teraz praktyka.
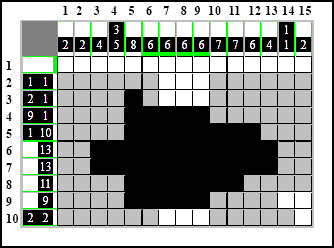
Przyjrzyjmy się kolumnie piętnastej. Znajduje się w niej tylko jeden element 2-kratkowy. Natomiast przez domalowanie białych okienek w dziewiątym wierszu spowodowaliśmy, że w kolumnie 15 powstała mała grupa pustych kratek. Dokładnie grupa 1-kratkowa na samym końcu tej kolumny. Ta grupa jest mniejsza od najmniejszego elementu w kolumnie piętnastej, który ma wielkość dwóch kratek. One się tam po prostu już nie zmieszczą! Możemy więc to miejsce zamalować na biało, ponieważ jest to pewne.
I to cała filozofia metody UNL.
Natomiast w kolumnie obok - w czternastej - nie możemy już tego zrobić, ponieważ tam najmniejszym elementem jest element 1-kratkowy i może on śmiało zmieścić się w pustym miejscu, które powstało na końcu tej pionowej linii. My zaznaczamy tylko rzeczy, których jesteśmy pewni na 100%.
Przejdźmy jednak do kolumny jeszcze wcześniejszej - do trzynastej i tam użyjmy metody "Uzupełnij Luki Pomiędzy Elementami"
Jak już zaznaczyłem, żeby skorzystać z tej metody potrzebna nam jest wiedza do jakiego elementu należy grupa kratek lub do jakich elementów - jeśli mamy zamiar zamalowywać puste miejsca pomiędzy elementami - czego w tym obrazku logicznym nie zrobimy, bo jest zbyt mało skomplikowany. Jednak zasada jest ta sama - zamalowujemy kratki poza zasięgiem elementów.
W kolumnie trzynastej możemy na dwa sposoby przekonać się, że grupa dwóch kratek należy do elementu 4-kratkowego.
Po pierwsze jest to jedyny element w tej kolumnie więc i grupa musi należeć do niego
Po drugie, jeśli skorzystamy z metody UPB (Uzupełnij Przy Przegach) i policzymy element maksymalnie od dołu w 13 wierszu, to "zahaczy" on sobą grupę dwóch kratek co oznacza, że ona po prostu do niego należy.
Skoro już wiemy z jakim elementem mamy do czynienia, użyjmy metody ULPE (Uzupełnij Luki Pomiędzy Elementami) w wariancie, że będziemy uzupełniać te luki pomiędzy jednym elementem a brzegiem diagramu.
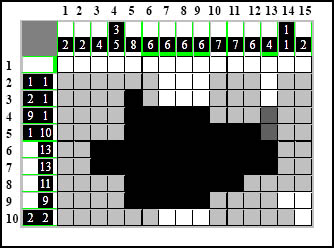
Czyli najpierw załóżmy, że element zaczyna się od dolnego miejsca, w którym zaczyna się grupa dwóch kratek - to jest od kratki czwartej licząc od dołu. Dodajemy brakujące dwie kratki i okazuje się, że elementowi zabraknie jeszcze dwóch kratek do krawędzi:
Teraz to samo tylko z przeciwnej strony: Zakładamy, że element zaczyna się od górnego miejsca grupy - to jest od szóstej kratki licząc od góry. Jak widać do końca braknie mu jeszcze jedna kratka, którą oczywiście zamalowujemy.
I znowu metoda UNL w wierszu dziesiątym.
Przez dodanie białej kratki w kolumnie trzynastej stworzyliśmy pustą lukę jednokratkową w wierszu dziasiątym, podczas gdy w tym wierszu najmniejszy element ma wartość 2 i nie zmieści się w luce. Zamalowujemy więc i to miejsce:
Powróćmy teraz na sam początek - do pierwszej metody "zazębiania" (MZ) i spróbujmy ją wykorzystać do oznaczenia elementów w dziesiątym wierszu, ponieważ przez to nasze domalowywanie, miejsca się w nim robi coraz mniej.
Najpierw jeden skraj - zaznaczamy dwa elementy każdy po dwie kratki:
Następnie druga strona, jak widać miejsca już nie starcza, aby ustawić dwa elementy obok siebie, jeden z nich trzeba przenieść dalej aby oba mogły się zmieścić.
Teraz sprawdzamy czy coś się zazębiło.
Zazębiło się, ale niestety nie to co chcieliśmy, ponieważ jak wiemy muszą się zazębiać te same elementy a nie różne.
Ponownie nic w tym wierszu teraz nie zaznaczymy. Musimy zaczekać jeszcze trochę.
Do tej pory poznaliśmy cztery podstawowe metody, które dodatkowo można rozbudowywać i modyfikować co spowoduje, że będziemy w stanie korzystając z nich rozwiązać znakomitą większość obrazków logicznych.
Metody te to:
1) Metoda Zazębiania (MZ).
2) Uzupełnij Przy Brzegach (UPB).
3) Uzupełnij Najmniejsze Luki (UNL).
4) Uzupełnij Luki Pomiędzy Elementami (ULPE).
Wracamy do malowania liczbami.
Ostatnio próbowaliśmy zdobyć jakieś kratki w ostatnim - 10 wierszu, lecz było na to jeszcze za wcześnie.
Przyjrzyjmy się jednak kolumnie czwartej z dwoma elementami - 3-kratkowym oraz 5-kratkowym.
Wykorzystajmy MZ ponownie. Licząc od skrajnej góry. Najpierw 3-kratkowy element:
Potem kratka odstępu i kolejny - drugi element 5-kratkowy - oba ściśnięte maksymalnie na górze:
Oznaczę cyframi dodatkowo dla lepszej widoczności:
Widać wyraźnie, że nawet maksymalnie ściśnięte zajmują sobą calutką linię co do jednej kratki. Właściwie nie trzeba już wcale liczyć od drugiej strony - po prostu nie ma innej możliwości ale oznaczmy to dla formalności. Czyli najpierw piątka od dołu a za nią trójka.
Oba zazębiają się w całości, nie pozostaje nic innego jak zaznaczyć to:
W drugim wierszu mamy same elementy o wielkości jednej kratki. Możemy więc w tym wierszu kratkę czarną - jaką przed chwilą zamalowaliśmy - dodatkowo obłożyć kratkami białymi z obu stron. Natomiast w wierszu trzecim widać, że powstał element 2-kratkowy, który z kolei jest pierwszy od lewej. Oznacza to, że mało tego iż możemy obwarować go białymi kratkami z obu stron (ponieważ wiemy, że to na pewno o niego chodzi) to jeszcze możemy uzupełnić białe kratki aż do samej lewej krawędzi diagramu - po prostu przed nim nie ma już nic innego:
Nie możemy namalować białych kratek z drugiej strony, ponieważ za elementem 2-kratkowym znajduje się 1-kratkowy i nie mamy pojęcia jeszcze gdzie on może być.
Dokładnie to samo dotyczy wiersza drugiego, gdzie powstało jedno puste pole, w które jednak zmieści się kolejny element 1-kratkowy w tym wierszu jednak...
Kiedy przyjrzymy się temu pustemu polu lecz z perspektywy szóstej kolumny, gdzie jest tylko jeden element 6-kratkowy, z łatwością wydedukujemy, że nie zmieści się tam szóstka i śmiało możemy zamalować puste miejsce (metoda uzupełnij najmniejsze luki).
Dodatkowo możemy uzupełnić tą kolumnę, ponieważ malując w wierszach uzupełniliśmy ją w całości do sześciu kratek.
Natomiast kiedy obwarowaliśmy element 1-kratkowy białymi kratkami z obu jego stron w wierszu drugim, jednocześnie postawiliśmy białą kratkę w kolumnie trzeciej i piątej. Ruchem tym sprawiliśmy, że teraz jedyne miejsce jakie zostało w piątej kolumnie zajmie do końca element 8-kratkowy.
Uzupełnienie nim linii do końca spowodowało, że w ostatnim - dziesiątym wierszu pojawił się w pełni wykształtowany;] element 2-kratkowy. Ponieważ tam są same elementy 2 -kratkowe, śmiało i jego możemy obwarować białymi polami po obu stronach.
Czyli podsumowując uzupełniamy do końca kolumny 5 i 6 oraz obwarowujemy element 2-kratkowy w 10 wierszu:
Przechodzimy do wiersza piątego, gdzie postawiliśmy białą kratkę odstępu. Ruchem tym spowodowaliśmy, że czarny element 10-kratkowy teraz zaczyna się dokładnie od białego pola i nie pozostaje nic innego jak po prostu przedłużenie go do samego końca - czyli do pełnych dziesięciu kratek. (jest to rozwinięcie metody "uzupełnij przy brzegach" - w tym przypadku brzeg stanowi ta biała kratka, o której wiemy, że na pewno stoi od lewej strony elementu 10-kratkowego, może zatem stanowić jego brzeg).
Przedłużamy więc:
Jedynkę po lewej stronie dziesiątki w tym wierszu natomiast nie wiemy jeszcze gdzie postawić, zostawiamy ją w spokoju.
Uzupełnienie elementu 10-kratkowego w wierszu piątym spowodowało pojawienie się jednej czarnej kratki w kolumnie czternastej, a ponieważ tam są same elementy 1-kratkowe, podobnie jak już to robiliśmy wcześniej, obwarowujemy czarne pole białymi po obu stronach.
Białe pola jak już wcześniej wspomniałem są tak samo ważne jak i czarne. W naszym przypadku postawienie białego pola w kolumnie czternastej spowodowało zablokowanie elementu 13-kratkowego w wierszu szóstym. Od tej pory nie ma on innej możliwości jak "iść" jedynie w lewą stronę. I tak go właśnie przedłużamy w lewo aż do samej jego długości, ponieważ dotyka go już brzeg z prawej strony.
Natomiast korzystając z metody ULPE w kolumnie pierwszej możemy oznaczyć białe kratki z jednej i drugiej strony grupy 1-kratkowej która się tu pojawiła:
Teraz już wiemy, że w dziesiątym wierszu na początku nie ma już miejsca na element 2-kratkowy i puste pole zamalowujemy na biało, natomiast korzystając z MZ oznaczamy część drugiego elementu 2-kratkowego w tym wierszu:
Metoda UPB i mamy calutką kolumnę jedenastą:
Skorzystajmy z tej samej metody w wierszu czwartym i policzmy od lewej element 9-kratkowy.
Najpierw dwa pola puste, potem sześć czarnych - razem osiem kratek. Brakuje jeszcze jednej. Ostatnia kratka wypada dokładnie pomiędzy grupą sześciu kratek i grupą jednokratkową. I nie ma innej możliwości na dodatek. Nie można już bardziej przesunąć w lewą stronę liczenia tak, żeby grupy pozostały osobno. Trzeba je po prostu połączyć ze sobą bo muszą należeć do elementu 9-kratkowego. W ten sposób, kiedy połączymy te grupy i korzystając z metody Uzupełnij Luki Pomiędzy Elementami" (w wariancie pomiędzy elementem i brzegiem), możemy domalować białe pole na początku tego wiersza:
Korzystając z tej samej metody uzupełniamy pola przy brzegach w kolumnie drugiej:
A potem metodą UPB uzupełniamy kratki w wierszach 8 i 9:
Teraz kolumna trzynasta... widzimy, że manewrami w wierszach doprowadziliśmy ją do końca - pojawił się w pełni wykształtowany;] element 4-kratkowy więc uzupełniamy resztę białymi polami:
Domalowanie przed chwilą białego pola w wierszu czwartym spowodowało, że pozostało już tylko jedno miejsce dla elementu 1-kratkowego więc go tam oznaczamy:
Ta kratka to zalążek elementu 2-kratkowego, na dodatek jedynego w kolumnie piętnastej, i na dodatek kratka ta zaczyna się od białego pola - a więc nie ma innej możliwości jak oznaczenie tego elementu w pełni oraz uzupełnienie kolumny białymi polami do końca:
Uzupełnienie piętnastej kolumny spowodowało pojawienie się czarnej kratki w wierszu trzecim a to oznacza, że pojawił się ostatni element w tym wierszu i resztę można zamalować na biało:
Kolumna dziesiąta - zamalowujemy puste pole bo nie zmieści się tam 7-kratkowy element.
W kolumnie dwunastej robimy to samo. Dzięki temu w wierszu drugim pozostało ostatnie pole na ostatni element 1-kratkowy. Oznaczamy to wszystko:
Pojawia się ostatni element w kolumnie czternastej - uzupełniamy resztę białymi polami.
Wszystko teraz pędzi z dużą prędkością i widać już metę...
Domalowane przed chwilą białe kratki blokują elementy w siódmym i ósmym wierszu, przez co możemy je przedłużyć do samego ich końca:
Pojawiają się końcowe elementy w pierwszej i drugiej kolumnie, uzupełniamy je:
Korzystamy z metody ULPE w kolumnie trzeciej licząc od dołu element 4-kratkowy i wyciskamy tym sposobem białą kratkę na górze tej kolumny:
Dzięki tej białej kratce uzupełniamy do końca wiersz czwarty:
A potem kolumnę dwunastą:
To pozwala nam uzupełnić do końca wiersze dziewiąty oraz dziesiąty:
Pozostaje ostatnie jedno puste pole, na ostatni element 1-kratkowy w wierszu piątym lub na dokończenie elementu 4-kratkowego w kolumnie trzeciej. Wszystko się zgadza!
No i nasza łamigłówka okazała się... ŚWINIĄ!;]
Kurs starałem się pisać przystępnie, krok po kroku.
Poznaliśmy w nim kilka ciekawych metod/sposobów myślenia/dedukcji - jak kto woli.
Teraz wystarczy zmodyfikować je nieco, ulepszyć, rozwinąć... no i bawić się rozwiązując kolejne obrazki logiczne!
I tego życzę wszystkim serdecznie na koniec.
Marcin Rejment